For further information about XPS/AES data processing please visit: http://www.casaxps.com/
Peak Fitting and Background Types with Example (HDPE, PEEK, Nylon)
Asymmetry in Polymer Peaks
Before using Asymmetric Line Shapes in Quantification, please read this PDF.
Line Shapes
A range of physically possible line profiles in core-level XPS is possible, and simple Gaussian or Lorentzian functions are very rarely adequate. In the case of metal samples it has been shown that asymmetric profiles should be expected on theoretical grounds [1], however recorded spectra exhibit deviations from idealized profiles due to a range of instrumental and physical effects:
1) The response function of the electron analyzer (which may be asymmetric),
2) The profile of the x-ray line-shape (predicted to be asymmetric for unmonochromatized metal anodes [1]),
3) Intrinsic life-time broadening of the core-level hole state (usually assumed to be Lorentzian in nature),
4) Phonon broadening,
5) Differential surface charging of the sample.
In addition to these instrumental considerations the shape of a synthetic peak is also influenced by the choice of background algorithm used to remove, so called, extrinsic electrons from the data. Figure 1 and Figure 2 are two examples of peak fits where the difference between the two outcomes lies in the choice of background. Doniach Sunjic profiles have been used to model the recorded doublet, where it has become necessary to adjust the asymmetry parameter as well as the width of the Gaussian used to broaden the underlying Doniach Sunjic shape. The most obvious difference between the two peak fits is the reduction in the amount of asymmetry required in the line-shape when a Shirley [2] background is used. This is best measured by the asymmetry index [1], which changes from 0.49 in the case of a linear background to 0.008 when a Shirley background is employed.
Although theoretically based, the Doniach Sunjic profile suffers from ill-defined areas. The integral of the Doniach Sunjic function is infinite for non-zero values of the asymmetry parameter [3] and therefore any direct use of this line-shape requires a somewhat arbitrary use of cut-offs to allow finite peak areas to be reported. Changing the shape of the peaks through adjustments to the asymmetry parameter and the width of the broadening function has altered the relative proportion of the spin-orbit split peaks in the Au 4f doublet (Figure 1 and Figure 2). The background choice has altered the reported intensity as well as FWHM for the individual peaks. These statements emphasize the importance of comparing like-with-like when quantification results are used in practice.
The choice of line-shape is determined by the nature of the problem. The best fit is not always as important as producing quantification results that can be compared to historical results. On the other hand if the results represent a sequence of experiments for which a trend is more important than the absolute values then a good model may take precedence over the need to supply numerical values consistent with the past. Provided the models are self consistent the use of Doniach Sunjic line-shapes may be acceptable.
Analysis driven by precise quantification lie at the route of many ad hoc procedures used in XPS. Shirley backgrounds were introduced precisely [4] to remove as much asymmetry as possible from recorded data (Figure 2) in a well-prescribed fashion, so that near symmetric synthetic models can be used to characterize the intensity under a peak. A Gaussian/Lorentzian line-shape is finite and, with the appropriate relative sensitivity factors (RSF), can be used to compare intensities from fitted peaks to those calculated from integration regions. The key factor that has popularized Shirley backgrounds is the availability of well-characterized RSF values coupled with a specific background and line-shapes.
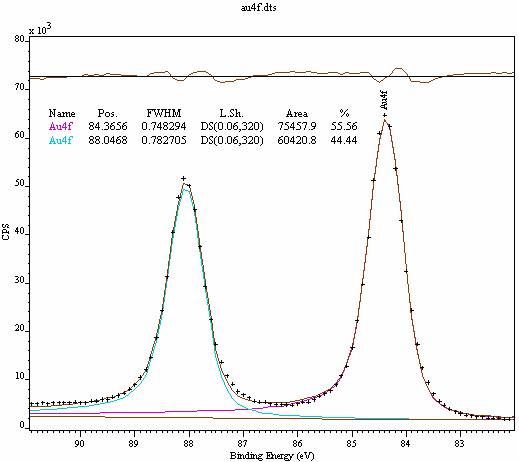
Figure 1: Au 4f doublet fitted using an offset linear background. The line-shape used in the fit is a Doniach Sunjic form convoluted with a Gaussian that results in an asymmetry index [1] of 0.49 for each peak.
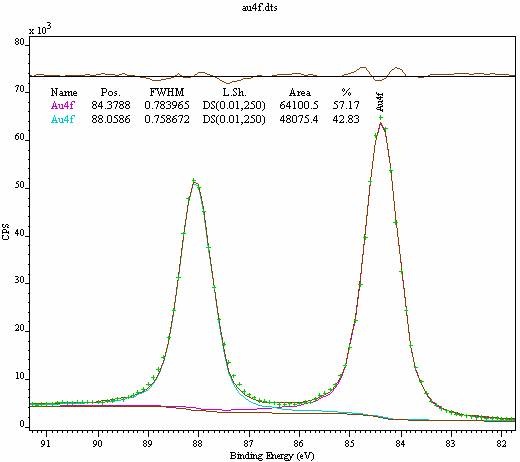
Figure 2: Au 4f doublet fitted using an iterated Shirley background. The line-shape used in the fit is a Doniach Sunjic form convoluted with a Gaussian that results in an asymmetry index [1] of 0.008 for each peak.
Some of the line-shapes introduced in CasaXPS have been constructed to allow Doniach Sunjic asymmetric behavior to be associated with an underlying Gaussian/Lorentzian shape. The Voigt approximation is used to characterize the area, position and FWHM, while the asymmetric form approximates the rise in the signal much in the same way that the Shirley background is used to reduce the data to symmetric shape. The advantage of retaining the asymmetry in the synthetic model is apparent when a Tougaard background is used to remove the extrinsic contribution to a metal spectrum.
To facilitate both trend analysis and basic quantification a wide range of line-shapes is required.
A List of Line-Shapes
The line-shapes offered in CasaXPS are based around the following fundamental functional forms.
The Voigt functional form has been the basis for most quantitative analysis of XPS spectra. Unfortunately, an analytic form for the convolution of a Gaussian with a Lorentzian is not available [3] and so practical systems have adopted two approximations to the true Voigt function.
Gaussian/Lorentzian Product Form
![]()
Gaussian/Lorentzian Sum Form
![]()
Exponential Asymmetric Blend Based upon Voigt-type Line-Shapes
Given either of the above Gaussian/Lorentzian symmetric line-shapes, an asymmetric profile is obtained from a blend function as follows.
![]()
Where
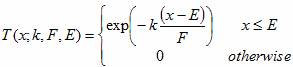
Alternative Asymmetric Line-Shapes
An asymmetric line-shape due to Ulrik
Gelius (
![]()
Where
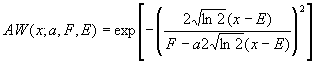
and
![]() .
.
The parameters a and b determine the shape of the asymmetric portion of the curve.
Doniach Sunjic: A Theoretically Based Asymmetric Line-Shape
Doniach Sunjic [1] performed an analysis for both photoemission and X-ray line-shapes, both of which result in an underlying profile given by the expression below. The formula includes an asymmetry parameter a that characterizes the asymmetry for a particular metal-like material. F is related to the FWHM and the position E is again related to but not equal to the position of the maximum intensity for the line-shape. It is therefore difficult to relate optimization parameters determined from the Doniach-Sunjic profile to similar quantities determined from Voigt-type line-shapes.
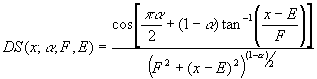
Nevertheless, the Doniach-Sunjic profile offers an asymmetric shape that is particularly appropriate for non-monochromatic X-ray induced transitions; the profile is potentially present in both the photoemission process as well as the excitation source.
Line-Shapes Based upon Backgrounds
The above profiles are assumed to be entirely due to intrinsic electron energy variations, where a background subtraction algorithm is required before these line-shapes can be used to model the spectra. An alternative approach is to include the background shape as part of the model [4]. An analytic form for the Shirley background can be determined for each of the line-shapes and the sum of these backgrounds plus line-shapes is used to approximate the variation in the spectrum. A simple constant background is all that is required for this procedure although other forms for the background are still an option.
Castle et al [4] have developed a Shirley-type adjustment to a Voigt line-shape. The Shirley approximation is calculated from the current Gaussian/Lorentzian shape and a polynomial b0+b1(x-E) is used to scale the background in order to provide a fit to the observed spectra. The procedure yields a “Kappa” parameter (given by b0) that characterizes the “intrinsic” step in the spectrum observed for a particular sample.
Line-Shapes Available in CasaXPS
Curve fitting in CasaXPS is performed via the Quantification Parameters dialog window where the synthetic line-shapes are defined from the scrolled-list on the Components property page (Figure 3).
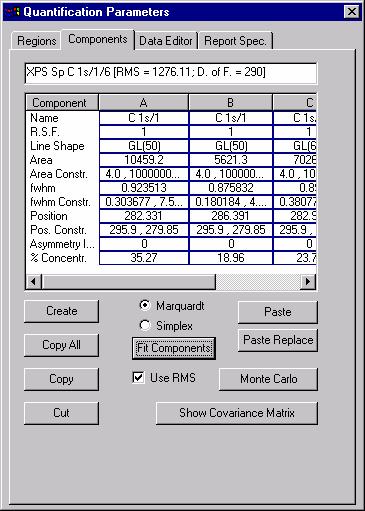
Figure 3: Property Page used to define synthetic line-shapes
The line-shape used to describe a photoelectric transition is entered in the row labeled “Line Shape” and takes the form of a text string.
GL(p) : Gaussian/Lorentzian product formula where the mixing is determined by m = p/100, GL(100) is a pure Lorentzian while GL(0) is pure Gaussian.
SGL(p) : Gaussian/Lorentzian sum formula where the mixing is determined by m = p/100, GL(100) is a pure Lorentzian while GL(0) is pure Gaussian.
GL(p)T(k) : Gaussian/Lorentzian product formula modified by the exponential blend.
SGL(p)T(k) : Gaussian/Lorentzian sum formula modified by the exponential blend
GL(p)K(b0,b1) : Gaussian/Lorentzian product formula modified by a Shirley-type background prescribed by Castle et al. A linear polynomial determined from b0 and b1 adjusts the step in the Shirley background.
SGL(p)K(b0,b1) : Gaussian/Lorentzian sum formula modified by a Shirley-type background prescribed by Castle et al. A linear polynomial determined from b0 and b1 adjusts the step in the Shirley background.
Further adjustments to the basic shapes
The basic shapes that result from the various functional forms can be further modified by numerically convoluting the profile with a Gaussian. For example, GL(100,50) will convolute a pure Lorentzian with a Gaussian characterized by a width of 50. The value for the width is the number of digital nodes used to describe the Gaussian and is therefore an arbitrary unit characteristic of the numerical form for the Gaussian.
N.B. Any line-shape that requires a digital convolution will cause slower performance than a shape that does not involve this procedure.
Asymmetric Line-Shapes
The exponential tail described by Sherwood in the book Practical Surface Analysis edited by Briggs and Seah attempts to approximate asymmetric line-shapes commonly found in photoelectric peaks. Several researchers have offered alternative deformations of the symmetric Voigt profile however none but Doniach Sunjic backs their approaches with a theoretical basis. Nevertheless, practical surface analysis requires practical solutions and the need for a rigid line-shape model that matches the observed profiles makes ad hoc forms acceptable tools. Philosophically, theoretically based solutions are preferred and hence, at least for metals, Doniach Sunjic profiles ought to offer “better” fits.
A practical solution offered by Ulrik Gelius (QSA 7) [5] uses a Voigt-like function as the underlying shape and modifies the lower kinetic energy electrons using the equations given above. CasaXPS offers these line-shapes in the form:
A(a,b,n)GL(p): Gaussian/Lorentzian product formula modified by an asymmetric form define above. The parameters a and b allow the asymptotic form of the asymmetric tail to change whilst also altering the shape of the asymmetry prior to attaining the asymptotic shape. Figure 4 shows one such class of profiles where the parameter a has been held fixed at 0.35 while b varies between 0.2 and 1. The third parameter n defines the width of a Gaussian used to convolute the basic shape of the profile.
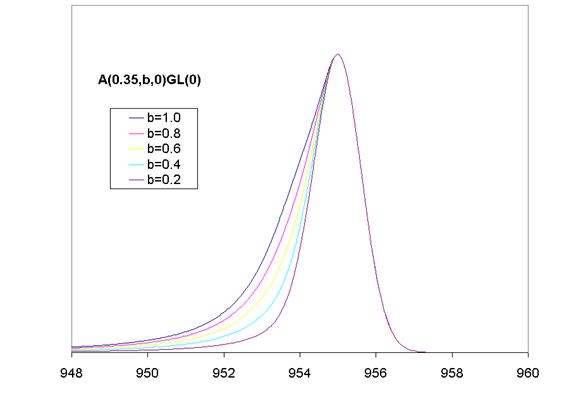
Figure 4: Asymmetric form due to Ulrik Gelius
The line-shapes defined by A(a,b,n)GL(p) and GL(p)K(b0,b1) are different from the Doniach Sunjic profile in that the Doniach-Sunjic profiles asymptotic limit is zero, while both of the ad hoc forms allow steps to be modeled within the line-shape itself. Another characteristic of these ad hoc line-shapes is that the peaks are defined in terms of intensity, position and FWHM taken from the underlying Voigt function. This is not unnatural in view of the fact that the area beneath all of these curves would be infinite without the introduction of some arbitrary cutoff limits.
DS(a,n): The basic Doniach Sunjic profile is defined in terms of the asymmetry parameter a and a convolution width n. The profile defined above is numerically convoluted with a Gaussian whose width is determined from n to produce the final line-shape.
Although the Doniach Sunjic line-shape allows very good fits to experimental data, the infinite intensity defined by the curve makes this profile difficult to use under practical situations. Any scheme that limits the area through cutoff functions or ranges introduces inconsistencies into the peak parameters that make relationships such as stoichiometry invalid. The degree of asymmetry used to describe the data moves intensity modeled by the line-shape away from the primary peak position and towards the cutoff regions (Figure 5). For this reason it is essential to use the Doniach Sunjic line-shape in situations where the asymmetry parameters are close to the same value so that calculated areas can, in some sense, be compared.
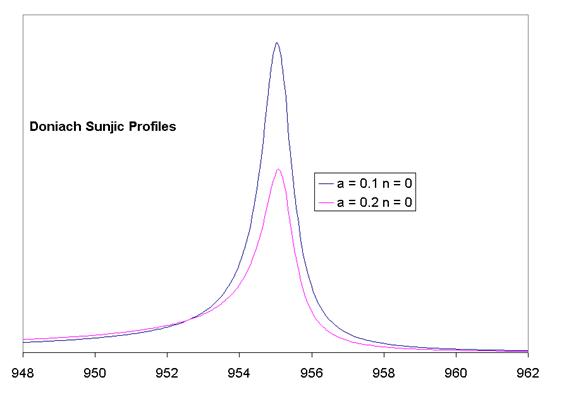
Figure 5: Doniach Sunjic profiles for asymmetry parameter equal to 0.1 and 0.2. Note how the asymptotic curves cross over illustrating how intensity is transferred away from the peak maximum.
Modifications to the Doniach Sunjic function
The advantages of the Doniach Sunjic profile are lost when synthetic models are required for quantification purposes. It is necessary to introduce ad hoc cutoff behavior before finite intensities can be reported and, once obtained, the peak areas can only be used in a quantification reports when relative sensitivity factors are know for the specific cutoff criterion adopted.
Empirical observations suggest that pure Doniach Sunjic profiles do not always yield good fits for electrons with higher kinetic energy (KE) when monochromatic X-ray sources are employed. For example, Al 2p doublets recorded using a monochromatic X-ray source appears less Lorentzian in nature (to the higher KE side of the peak) than the Doniach Sunjic shape will allow (Figure 6), however the same line measured using an Aluminium anode does exhibit the predicted (but somewhat broader) shape. The latter is thought to be due to the double influence of the Doniach Sunjic shape from the photoemission process as well as the X-ray line profile, while monochromatic X-rays have lost the Doniach Sunjic distribution as a consequence of the filtering process.
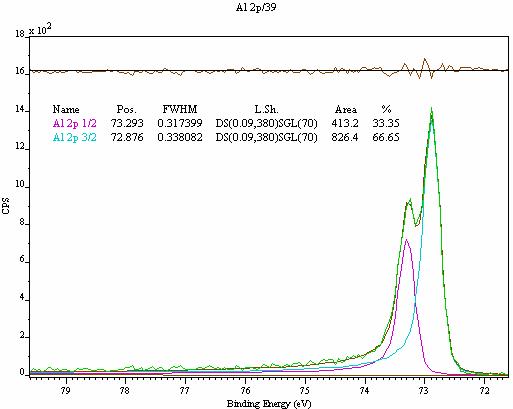
Figure 6:Al 2p Doublet from a monochromatic X-ray source.
In order to fit spectra such as that shown in Figure 6 the pure Doniach Sunjic shape has been modified. The lower KE asymmetry derives from the functional form for the Doniach Sunjic profile while the higher KE side of each component is a Voigt-type function. A numerical convolution is applied to the combined profiles to produce the line-shapes in Figure 6.
Given an approximation to the Doniach Sunjic profile of the form shown in Figure 6 then the possibility of characterizing the line-shape by the associated Voigt-type profile becomes feasible. The Voigt-type portion of the line-shape provides the position, width and intensity while an asymmetry index [1] measures the departure of the line-shape from a symmetric form. Such a regime fits well with the philosophy adopted by Shirley, where the background shape was used to reduce an asymmetric step to a form that could be characterized by a Voigt function. The asymmetry index is given by
![]()
The asymmetry index is reported on the Components Property Page for each line-shape.
H(a,n)GL(p): Hybrid Doniach Sunjic/Gaussian-Lorentzian(product) line-shape.
H(a,n)SGL(p): Hybrid Doniach Sunjic/Gaussian-Lorentzian(sum) line-shape.
The “H” form of the DS/GL hybrid line-shape is identical to the DS(a,n)GL(p) form except the position, FWHM and area parameters are all determined from the Voigt-type shape. Compare the area values reported in Figure 7 to those from Figure 6. The area taken from the Voigt-type portion is significantly less than the intensity taken from the Doniach Sunjic curve where a cutoff has been used. Another difference between the two forms is that the area reported by the “H” is much less sensitive to adjustments in the asymmetry parameter (numerical convolution does move shape information between the two halves of the line-shape).
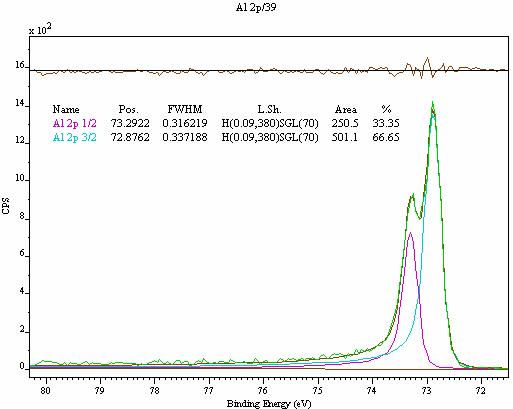
Figure 7: Hybrid DS/GL line-shape characterized by the Voigt-type portion.
A New Line-Shape
The hybrid form of a DS/GL line-shape is blended using a numerical convolution. The maximum for the two shapes diverge for larger asymmetry values, therefore characterizing the peak parameters by the Voigt-type portion is more difficult as the asymmetry becomes more pronounced. A new class of functions can be introduced to over come this problem, namely, a set of line-shapes that are a blend of the asymptotic behavior from the DS line-shape with a Lorentzian.
The cosine term in the Doniach Sunjic profile rapidly approximates a step function as the asymmetry parameter increases, while for small values of this parameter the cosine term is responsible for the movements in the DS maximum and for a = 0 results in a pure Lorentzian form. The formula for the “F” profile combines these characteristics by blending the asymptotic behavior of the DS profile with one of the Voigt-type functions using a linear mapping.
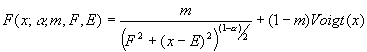
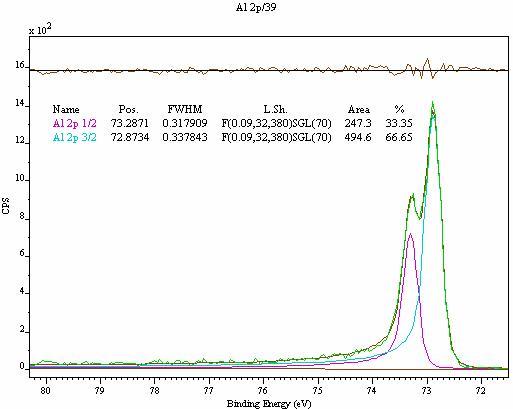
Figure 8:A new line-shape that blends the asymptotic behavior of a Doniach Sunjic profile with a Voigt-type function.
F(a,m,n)GL(p): Asymptotic Doniach Sunjic/Gaussian-Lorentzian(product) linear mapping line-shape.
F(a,m,n)SGL(p): Asymptotic Doniach Sunjic/Gaussian-Lorentzian(sum) linear mapping line-shape.
The linear mapping between the two functional forms is defined as a percentage through the m parameter. Figure 8 shows the same Al 2p data envelope as is seen in Figure 7, but the line-shapes are defined using the “F” functional form. In Figure 8, the same asymmetry value has been used as the one in Figure 7 however the linear mapping parameter is set to 32% DS asymptotic form 68% Voigt-type function. The resulting profile is convoluted with a relatively wide Gaussian (characterized by the number 380) and accounts for the Lorentzian bias in the Voigt approximation.
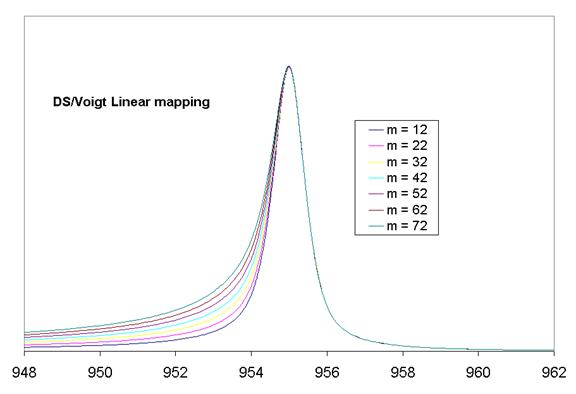
Figure 9: "F" function plotted over a range of values for the linear mapping parameter, a constant asymmetry parameter (0.09) and no numerical convolution applied.
Figure 9 shows how a pure Voigt-type function, SGL(70), is merged with the asymptotic form for a Doniach Sunjic profile (asymmetry parameter equal to 0.09) for a range of the linear mapping parameter. The characteristic shape of the Doniach Sunjic profile can be retained to some degree but is supplemented by a class of shapes that go beyond what is possible with a DS profile. The principal difference between the DS profile and the “F” function lies in the static position of the maximum for the class of profiles. The moving maximum is a feature of the DS profile and can be achieved to some extent by use of the numerical convolution option. Increasing the width of the Gaussian caused the line-shape to lean in towards the asymmetric side of the peak (Figure 8).
A further variation on a theme is also possible where the “F” function can be replaced by:
![]()
The “E” function is merely allows the shape to the right to be a part of the asymmetric shape to the left.
Background Subtraction
The line-shapes described above are very dependant on the availability of background subtraction algorithms that complement their use. If a background is incorrectly removed from a spectrum then the merit of attempting to model the result with theoretically correct synthetic line-shape is less clear.
Tougaard and co-workers [6] have devoted much time to understanding the backgrounds that are present in XPS spectra. The transport of electrons through a material after excitation by X-rays can be described by equations [7] that involve a one-sided convolution of the recorded data with an energy-loss probability distribution. This loss function offers a prescription by which electrons leaving the sample with an initial energy may have their characteristic energy altered by the interactions with the surface. Each material has a characteristic loss function of varying complexity and Tougaard has written many papers describing methods for establishing both generally applicable approximations (so called, universal cross-sections) and specific forms for individual materials.
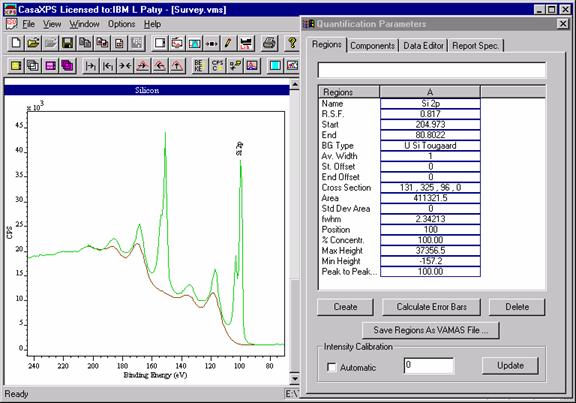
Figure 10:Three-parameter universal cross-section for Silicon
The principal methods used by Tougaard for calculating the loss functions are theoretical dielectric response models and empirical estimates computed from spectra acquired using reflected energy-loss spectroscopy (REELS). Tougaard follows these calculations by fitting the results to a rational function, which models the resonance structure in the calculated loss-functions and allows the essential distribution to be described by a simple formula. These loss-functions are defined in terms of four parameters, three of which describe the shape of the rational function and one to allow for various band gaps in different materials. Tougaard refers to the distribution below as a “three-parameter universal cross-section” and has established values for a number of materials including Aluminium, Silicon, Silicon Dioxide and others [6]. The form of this universal cross-section is
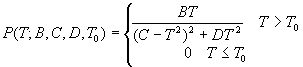
CasaXPS offers several ways of using the three-parameter universal cross-sections. The background type defined on the Regions Property Page of the Quantification Parameters dialog window (Figure 10) may be chosen from the following list:
U Si Tougaard
short form U Si:
Three-parameter cross-section determined for Silicon.
U SiO2 Tougaard short form U SiO2: Three-parameter cross-section determined for
Silicon Dioxide.
U Al Tougaard short form U Al : Three-parameter cross-section determined for Aluminium.
U Ge Tougaard
short form U Ge:
Three-parameter cross-section determined for Germanium.
U Poly Tougaard short form U Poly: Three-parameter cross-section determined for
Polymers.
U 4 Tougaard short form U 4: Custom three-parameter cross-section where the
parameters are entered on the Regions Property Page (Figure 10) in the Cross
Section text-field. The four numerical values entered in a comma separated list
correspond to B,C, D and T0 in the energy-loss function above.
C 4 Tougaard short form C 4: Alternative custom three-parameter cross-section
where the parameters are entered on the Regions Property Page (Figure 10) in the
Cross Section text-field. The four numerical values have the same meaning as
those found in the U 4 Tougaard form, however T0 is used to shift
the resonance structure rather than simple acting as a cutoff limit. It is
therefore possible to retain the shape of the distribution but move the
position of the maximum without changing the C and D parameters.
The custom Tougaard cross-sections offer a chance to change the background in response to the spectrum under investigation. Such an approach is not unprecedented [8]. “Direct, simultaneous determination of XPS background and inelastic differential cross sections using Tougaard’s algorithm” by Dr. M. Jo describes a method that extracts loss-functions from the XPS data using optimization procedures applied to a cross-section defined in terms of Spline polynomials.
The rigid model offered by the three-parameter cross-section provides more guidance in the regions most influential in peak fitting, but will struggle to reproduce the asymptotic behavior for the cross-section as well as the adjustments needed to describe the near peak region of the background. Nevertheless, a practical approach to the use of Tougaard backgrounds in peak fitting is to choose a background that works in conjunction with the synthetic peaks. The custom form for the cross-section allows the background to develop at the same time as the peak parameters and choice of line-shapes. Figures 6 through 8 all use a custom three-parameter universal cross-section to describe the background under an Al 2p metal doublet; typically, researchers would choose Shirley background for such spectra.
Adjusting the three-parameter universal cross-section
The rational function for the three-parameter cross-section is defined in terms of three constants B, C and D. This approximation is the quotient of a linear polynomial and a quadratic in terms of T2, but it is the denominator that determines the position and strength of the resonance in the cross-section. The parameters C and D both determine the position, width and height of the resonance, but to a first order (small D) the position is influenced by the square root of C and the sharpness of the cross-section is determined from the size of D.
The distance of a complex pole from the real-line in the domain of a complex function is instrumental in determining the width of a resonance when the function is plotted with respect to a real variable. The D parameter principally moves the poles of the Tougaard cross-section away from the real-line, while C changes the projection of the pole onto the real-line. Small D corresponds to near singular behavior in the cross-section and therefore results in shape structures located, to some degree, by C while the magnitude of the function can be moderated by adjusting the B parameter. It should be noted, however, that B adjusts the behavior of the cross-section in the region close to zero energy-loss. This is precisely the region of interest for modeling a peak and so the values given to B and D can be influential in obtaining a reasonable synthetic model.
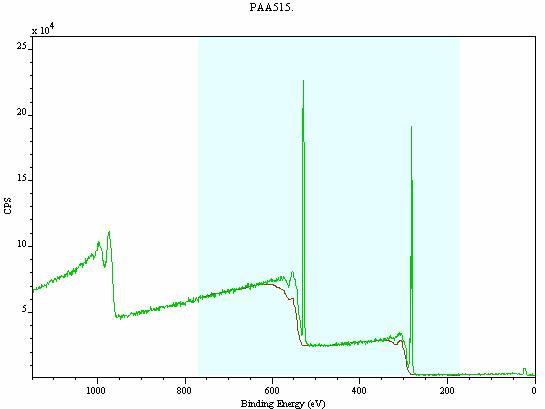
Figure 11: Wide scan spectrum from a PAA sample with a custom three-parameter cross-section applied.
The three-parameter universal cross-sections for specific materials may be used as a basis for determining a background. A wide scan spectrum allows the essential form for a background to be determined in the case of materials for which cross-sections are not available. The resulting background is easily transferred to any high-resolution spectra from the same sample (Figure 11 and Figure 12).
The meaning attributed to custom backgrounds should be viewed in the same way a synthetic model for a peak envelope is viewed. That is to say, only chemistry and knowledge of the sample allows a synthetic model to be constructed which has any meaning and this should also be the case for custom Tougaard backgrounds. The use of these backgrounds is entirely at the discretion of a researcher and bad backgrounds can be constructed in much the same way that synthetic models are open to abuse. However, a carefully constructed background can reveal features that may be overlooked or not accessible when a linear or Shirley form is applied. Figure 12 shows an O 1s structure from PAA (poly(acrylic acid)) after a custom Tougaard background has been subtracted. The structures to the deeper binding energy side of the peak may be real or an artifact of the background algorithm, but a linear background applied to the same data would fail to ask any questions at all regarding these features.
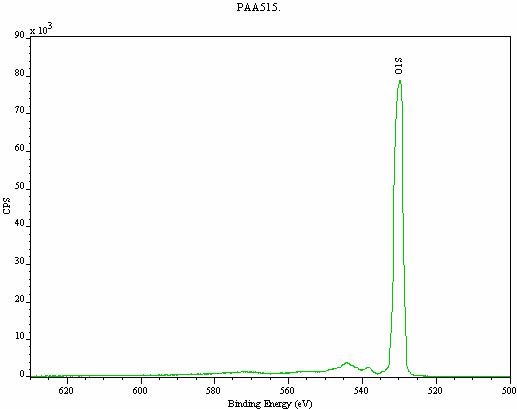
Figure 12: High-resolution spectrum from the same PAA sample shown in Figure 11. The custom Tougaard background has been subtracted from the data.
Simulating Spectra using Custom Tougaard Backgrounds
Given a set of synthetic peaks and a three-parameter universal cross-section it is possible to construct a spectrum with an associated background. The synthetic PAA spectrum in Figure 13 has been constructed from a set of Gaussian/Lorentzian line-shapes approximately positioned at the experimental values for the valance band, two C1s structures, two O AES peaks and one O 1s photoelectric peak. The widths and intensities are consistent with results for such a sample measured using a Scienta ESCA-300 at RUSTI, Daresbury Laboratory, UK, and the cross-section has been chosen similar to the one used in Figure 12. A sequence of iterations using these peaks and the three-parameter universal cross-section shown in Figure 14 converges to the synthetic spectrum in Figure 13.
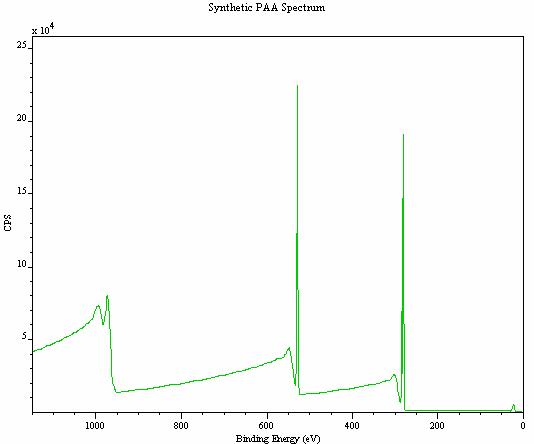
Figure 13: Synthetic PAA spectrum constructed from a set of Gaussian/Lorentzian line-shapes and a custom Tougaard cross-section.
This technique for generating theoretical spectra offers a way to understand the consequences of choosing a particular cross-section and if nothing else provides a basis from which real spectra can be viewed. Surface morphology and nano-structure causes most real spectra to exhibit background behavior that is not characteristic of a material but the environment in which the element is found. Attempting to construct a spectrum based purely on a resonant cross-section model clearly shows the limitations of such approximations when applied to real samples.
Although synthetic modeling has little direct use for real samples, it does offer an analyst the opportunity to investigate algorithms used to probe real spectra. For example, numerous techniques have been proposed from Multivariate Statistics for reducing XPS spectra to meaningful chemical information [9] [10]. Procedures for generating simulated spectra allow data sets to be constructed with similar characteristics to the experimental data but with well-defined information. These algorithms can be applied to the simulated spectra in order to establish what information is extracted for a perfectly understood data set.
Everyday procedures such as curve fitting can be evaluated using simulated spectra and therefore the ability to produce spectra with known shapes can enhance understanding for students and researchers alike.
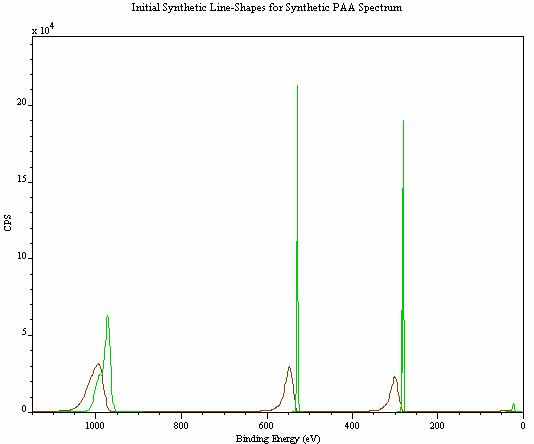
Figure 14:Initial synthetic components used to construct a PAA spectrum (green). The background curve (brown) represents the first iteration of the cross-section with the model data.
[1] Doniach S. and Sunjic M., J. Phys. 4C31, 285 (1970)
[2] Shirley D. A., Phys. Rev., 55, 4709 (1972)
[3] Evans S., Surf. Interface Anal., 17, 85 (1991)
[4] Castle J. E. et al, J. Electr. Spectr. Related Phenom,106, 65 (2000)
[5] G. Wertheim, J. Electron Spectrosc. 6, 239 (1975)
[6] Tougaard S., Surf. Interface Anal., 25 137 (1997)
[7] Tougaard S., Surf. Interface Anal., 11 453 (1988)
[8] Jo M., Surface Science, 320 191 (1994)
[9] Fiedor J.N., Proctor A., Houalla M. and Hercules D.M., Surf. Interface Anal.,20 1 (1993)
[10] Do T., McIntyre N.S., Harshman R.A., Lundy M.E. and Splinter S.J., Surf. Interface Anal., 27, 618 (1999)