SVD Sorting: Images, Spectra and Information Combing
By Neal Fairley
Abstract:
Statistical techniques are described for
efficiently reducing noise from data. An algorithm for partitioning useful
information from the noise within a set of measurements is presented and its
implications for XPS acquisition strategies are discussed.
When
constructing an experiment, the aim is to acquire data for a sufficiently long
period to permit the computation of reliable quantitative values. This precision
requirement must be balanced against efficient use of instrument time and
therefore acquisition times should be optimal for the desire outcome. If an
experiment can be constructed in which the acquisition time is split between
multiple variables (energy, position, etch-time etc), all of which useful to
the analysis, then statistical techniques can be used to synthesis the signal
from the noise on mass, rather than obtaining a given signal-to-noise via devoting
instrument time to each individual measurement.
A paradigm
for such an experiment is one in which a set of XPS images are acquired over a
sequence of energy setting. The result is an image, where each pixel offers a
spectrum of energy information. The acquisition time for such an experiment is
relatively large as a whole; however on an individual spectrum-at-a-pixel basis
the acquisition time is small. As a result the signal-to-noise for individual
spectra is poor and therefore the data are not suitable for determination of
quantitative results. Ignoring the spatial variation in these spectra by simply
summing the energy channels across the image produces a spectrum with good
signal-to-noise, but without the original spatial information. The problem is
therefore to synthesis the noise from the pixel spectra without loosing the
spatial information originally present in the data set. Such analyses are the
realms of multivariate statistics and linear algebra, since with the aid of
these tools the effective noise in any one spectrum can be reduced to yield
remarkable results.
Synthetic Data Set
To
illustrate the discussion points, a set of synthetic spectra were constructed
from five Gaussian line shapes, where spatial variation is simulated by
adjusting the area of the Gaussians using sinusoidal functions parametrically
dependent on the pixel position. Figure 1 shows the relative positions of the
five Gaussian peaks with respect to energy; all five synthetic peaks were
assigned the same full-width-half-maximum.
Using this basic structure, simulated noise consistent with XPS data was
used to generate five additional set of image data sets, where the intensity
per bin is scaled by a factor of two across the set of five data sets. Since
the noise for XPS data varies as a function of the square root of the counts
per channel, the signal-to-noise ratio improves throughout the sequence of data
sets (Figure 2).
These
synthetic image data sets contain a 96 by 96 array of spectra in which each
spectrum includes 100 energy channels.
Vector
Spaces
While the
data shown in Figure 2 are intended to look like XPS spectra, the partitioning
of such data into useful information and noise is performed using techniques
from linear algebra. Therefore the spectra are viewed as vectors in an m-dimensional
vector space, where m is equal to the number of bins per spectrum. The
objective is to determine a set of vectors representative of the useful
information, yet belonging to the same m-dimensional vector space as the
original set of vectors, and use this subset to model each and every vector in
the original data set. The hopes is that the complementary subset contains just
the noise component in the data and so by excluding these noise vectors when
modelling the raw data, the resulting vectors will be a noise free set of spectra.
The partitioning of the vector space is almost never perfect and so the
procedure typically yields improved signal-to-noise statistics, not a complete
elimination of the noise.
The
conventional method for constructing a set of vectors spanning the same
subspace as the original vector space is an eigenanalysis based upon the
covariance matrix (Equations 1 and 2). The covariance matrix is formed from the
dot product of the original vectors and is therefore a real symmetric matrix. The
result of an eigenanalysis is an orthogonal set of eigenvectors, where the information
content in each of the eigenvectors is ranked by their eigenvalue. This ranking
of the eigenvectors allows the significant
information to be collected into a relatively small number of vectors from
a much larger, but over specified set of vectors. These significant vectors,
when constructed via the covariance matrix, are referred to as the Principal
Components and hence the decomposition into these new vectors is often called
Principal Component Analysis (PCA). What is more, the decomposition of a set of
vectors using the Singular Valued Decomposition shown in Equation 3 is directly
related to the linear least squares principle and explains why the data is
transformed into an ordered set based on information content. Computing the
improved set of spectra, with respect to noise content, is achieved by choosing
to set the wkk equal to zero for all k above or equal to some value in
Equation 3, where the nonzero wkk below
the chosen value of k correspond to
the vectors containing the principal components.
The caveat
in the previous discussion when applied to the sets of spectra-at-pixels is the
shear quantity of spectra. Given the synthetic data set described above, the
vector subspace would be of maximum dimension 100, that is, the number of
energy channels per spectrum, while the total number of spectra involved in the
calculation is 962, or 9216. Forming the covariance matrix from the
data matrix prescribed in Equation 2 would result in a matrix of size 9216 by
9216. Alternatively the covariance matrix could be formed from post
multiplication by the transpose of the data matrix resulting in a covariance
matrix of size 100 by 100. The success of any noise reduction is achieved by a
comparison of information in a least squares sense and, as with all least
squares calculations, the number of such samples influences the precision of
the result. Forming the larger of these two covariance matrices represents the
situation where the least squares procedure acts on an energy-channel by
energy-channel basis, while the smaller covariance matrix corresponds to the
least squares criterion acting on a pixel-by-pixel basis. That is to say, the
averaging effect of the least-squares criterion has considerably more data with
which to work when using the 9216 by 9216 covariance matrix. However, there are
few with computers capable of performing a direct SVD to a problem of this
size. Yet, if the original data are numerous poor signal-to-noise spectra, the
use of large numbers of data points for the least-squares procedure is highly
desirable. In this sense, an alternative to direct PCA is required.
SVD
Sorting
SVD sorting
is an algorithm for moving significant vectors to the top of a list of vectors,
where the loop invariant when scanning through the set of vectors is the
following: the set of vectors all remain within the same subspace spanned by
the original set of vectors. The idea is to compare adjacent vectors by
computing the eigenvectors and eigenvalues, transforming the vectors in the
process, which effectively moves the most significant transformed vector up the
list in an analogous way to the Bubble Sort algorithm for ordering keys. The
result of stepping through the set of vectors once is that the most significant
information is moved up the list in the form of a transformed vector. This
procedure employs the same mechanism as SVD to transform the vectors en route,
however the size of the SVD is always two and therefore, for a single scan
through the set of vectors, the computational complexity is O (n), where n is the number of vectors. The number of scans applied to the data
set is then dependent on the number of components within the set of vectors and
can be chosen for a given application. Bubble Sort is an O (n2) algorithm; similarly for
SVD Sorting, after n scans the vectors would be fully ordered according to this
pair wise comparison, however the difference between a full SVD based PCA and
SVD Sorting is the final set of vectors are not mutually orthogonal and it is
relaxing this mutually orthogonality constraint that
yields the reduction in time spent on computation. The fact that the resulting
set of vectors is not necessarily mutually orthogonal is only a problem if
there are no dominant vector directions; in which case, the PCA would have been
of little value anyway. Moving the variation in the vector set to the top of
the list allows the useful vectors to be identified and a full SVD can be
performed on these data to yield the PCA quantities. Since in general, the
number of significant factors is small compared to the overall data set size,
the use of a selective PCA via a SVD is time efficient.
The
essential steps used in an SVD scan are illustrated in Algorithm 1. Repeated
applications of these steps orders the information content in a set of vectors
until finally, the important vectors to the description of the subspace, appear
at the top of the vector list. Isolating these vectors and applying a standard
SVD to only these significant vectors is equivalent to generating the matrices
in Equation 3 but where the unwanted wkk
are already set to zero.
Results
Apart from
achieving the same result as a massive SVD in a shorter time, the real
significance is that the least-squares criterion has been applied in the most
advantageous order for removing the noise on an energy channel basis. The
consequence of which is that abstract factors containing minor adjustments to
the overall description of the spectra will be less likely to include major
features due to noise. Thus, more abstract factors can be included in the
reconstruction step without reintroducing a significant noise component and so
achieve a better approximation to the original data. Figure 3 illustrates the
results of applying the combination of:
1.
SVD
sorting followed by,
2.
a
PCA on a small number of sorted vectors and
3.
finally reconstructing
the spectra from the five most significant abstract factors.
These steps have been applied to
the image set in which the signal-to-noise is the worst of those shown in
Figure 2. Once reconstructed spectra are computed for each pixel; simply
placing integration regions on the spectra and calculating images using the
intensity from these five regions (labelled P1 through P5 in Figure 1), a set
of spatially resolved quantitative values result (Figure 4). The images in
Figure 4 are computed for each of the five sets of data in which the
signal-to-noise varies, plus the PCA enhanced spectra as well as the exact
spectra (Figure1). Visual inspection shows the PCA enhanced image is equivalent
to the image simulated to have four times the intensity as the data used in the
PCA procedure.
Conclusion
For XPS there are two major implications. Firstly, the acquisition time
for a given precision can be reduce by roughly a factor of four (provided
sufficient information is still present in the data set as a whole) and
secondly, the PCA enhanced spectra offer a superior definition for the
background to the spectra and consequently the resultant images are free from
artefacts often associated from background variations. What is more, the
improvements in the background also open up the opportunity to use background
information to extract thickness of layered structure on the sample surface.
Application of simple techniques proposed by Tougaard
in cases where the background above and below a peak is well define offers
alternative image processing resulting in topographical maps.
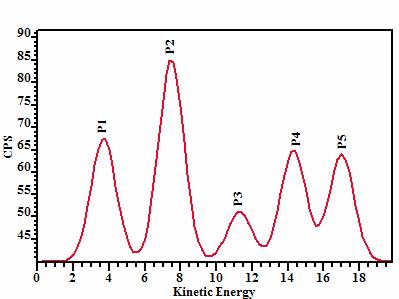
Figure 1: Synthetic data envelope constructed from Gaussians.
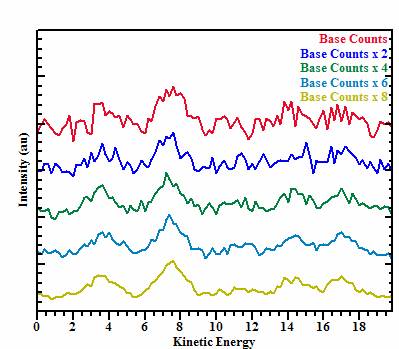
Figure 2: These spectra correspond to the synthetic envelope in Figure 1, where random noise is added on the basis that the intensity per channel varies by a factor of two throughout the sequence bottom to top.
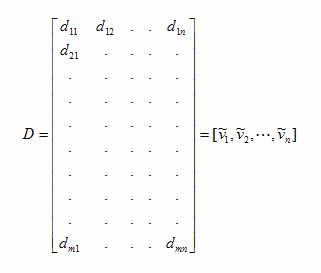
Equation 1
![]()
Equation 2

Equation 3
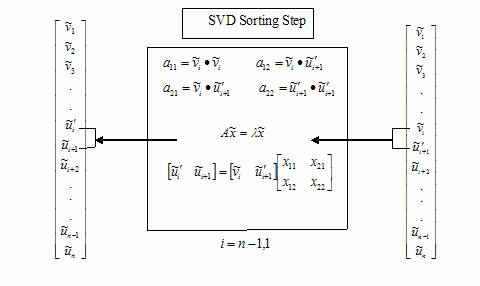
Algorithm 1
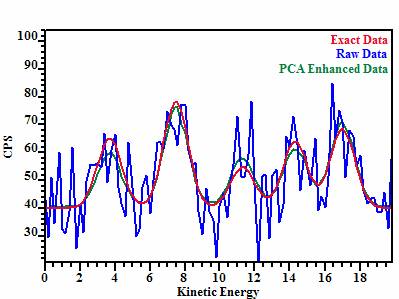
Figure 3
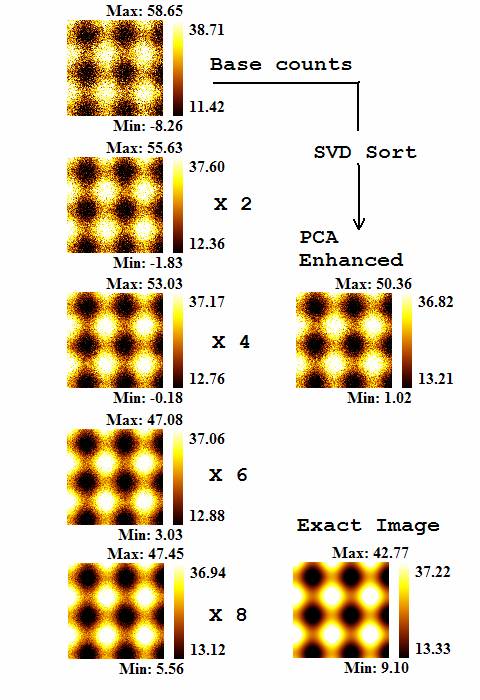
Figure 4